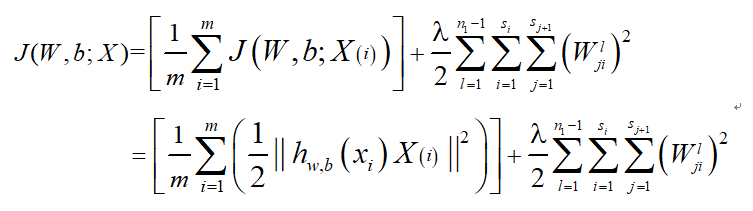无监督的稀疏自编码器可以自动化地提取出稳定的高维特征，同时小波分析（Wavelet）对金融时间序列数据去噪效果显著，通过在智能选股场景中将二者结合起来，发现新的深度学习网络结构（WaveleT+SSAE）可以更有效地控制组合的回撤幅度，在2017年前后不同的市场风格下，该算法都展现出来良好的风险控制能力。

一、无监督学习算法的广阔应用前景

近年来，深度学习技术在图像识别，语音识别，自然语言处理，股价预测，天气预测，内容推荐等各个领域都得到了广泛应用，然而随着有监督学习的低枝果实被采摘的所剩无几，无监督学习成为了未来研究热点。特别是在涉及特征提取的特征工程中，无监督学习算法因为其自动化的特征提取以及在提取稳定和高维特征上的优异表现而吸引越来越多的研究者投身其中，甚至与GAN(生成式对抗神经网络)并驾齐驱，延伸出很多有趣的应用。有下图可见一斑：左图是 FIFA18中的C罗的真实图像，右边图像是由一个深度自编码神经网络生成的C罗图像，深度自编码网络在提取了真实图像的特征之后依据这些特征自动生成了高度相似的右边C罗的图像，可以达到以假乱真的程度。

图1. C罗脸部图像对比

与此同时，AI相关算法在金融领域也得到广泛深入的应用，17年10月18日更是诞生了全球第一只应用人工智能、机器学习进行投资的ETF：AI Powered Equity ETF，其依据EquBot独门算法所打造出来的主动式ETF，利用IBM Watson的认知和大数据处理能力去分析美国境内的投资机会。发行至今，在这轮的美股大牛市中除了稍逊色于最强势的纳斯达克指数外（15%VS17%），AIEQ大幅战胜道琼斯工业指数和标普500，显示了强大的学习能力，从而引发市场对AI相关算法在投资分析、预测方面产生了更多期待。

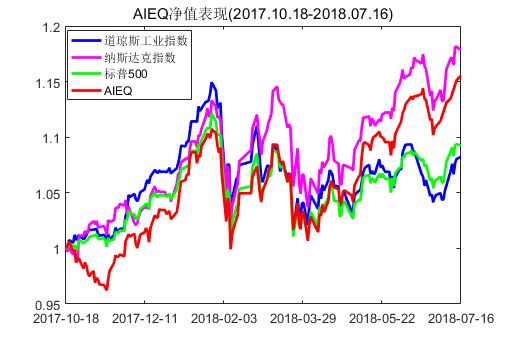
图2. AIEQ和基准收益对比

二、堆栈稀疏自编码器的算法原理简介

在智能选股相关算法产品研发过程中，我们尝试引进在无监督学习中更为基础且表现良好的编码器算法-堆栈式稀疏自编码器（SSAE：Stacked Sparse AutoEncoders）。假设自编码器输入层和输出层神经元的数目相同，通过隐含层网络使输入和输出层的误差最小，从而确保可提取出最能代表原始数据的特征。其具体的网络结构如下：

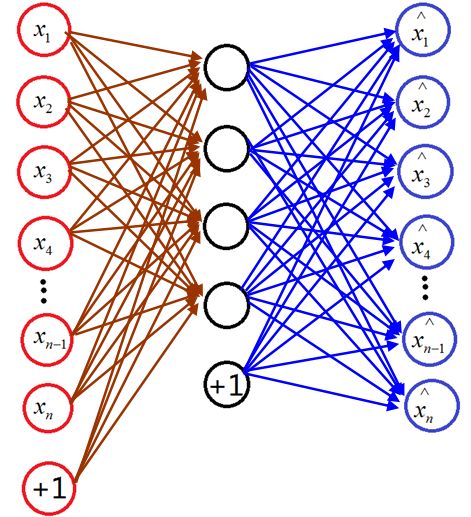
图3. 自编码器（AE）的网络结构

如果去掉输出层以后，隐含层的值就是我们需要求的特征值，假如有n个输入，隐含层有m个神经元，输出层也为n，那么此网络有m个特征值，然后再接上softmax分类器就形成了Sparse Autoencoder-Softmax分类器模型。而堆栈式编码器通过逐层堆叠，前一层的特征值作为下一层的输入，层层提取，层层去噪，可以提取更稳定的高维特征。

自编器网络结构的算法目标也在于最小化输入、输出的损失函数，而自编码器网络的独特之处在于其输入和输出特征经提取训练后数量上仍然相等，且能提取出最能代表输入数据的特征。假设输入向量为X，那么通过稀疏自编码（Sparse Autoencoder） 网络输出向量Y在数量上与X的数量相等，假如给定m个样本，加上正则项，损失函数可以写为：

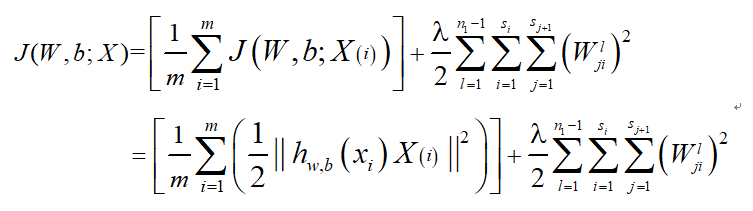
自编码器通过前向传播得出损失函数，再通过后向传播使特征值的重构值和输入数据之间的损失函数最小化从而不断优化网络权重，提取出最稳定的数据特征。

三、小波分析（Wavelet）的算法原理

由于金融市场中各种偶然因素的影响，使得金融数据，特别是金融时间序列数据中存在许多噪声。这些噪声严重影响了数据进一步的分析和处理，有必要预先去噪。但是金融时间序列本身具有非平稳、非线性和信噪比低的特点，采用传统的去噪处理方法往往存在诸多缺陷。

小波理论则是根据时频局部化的要求而发展起来的，具有自适应性和数学显微镜性质，特别适合对非平稳、非线性信号的处理。如下图，图4为原始信号，为时域和频域的混合，而通过3层小波变换成为图5，原始信号可以同时清晰的呈现为时域和频域两个维度上特征,X轴为频率，Y轴表示时域，Z轴表示振幅。在图5中，任意坐标轴空间内的点都对应1对时域和频域内的特征值，表示信号在某个时点的频率特征，高频对应的是信号中的噪声，也可理解为短期扰动，图中显示为频域最上面的红色部分，低频则对应信号中包含的主要信息，也可理解为趋势信息，图中显示为频域最下面的黄色部分，蓝色部分则介于二者之间，因此通过小波分析可以将信号层层分解为趋势信息和噪声扰动，清晰呈现信号本质。

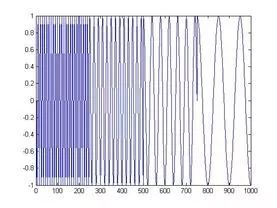
图 4. 金融市场原始信号

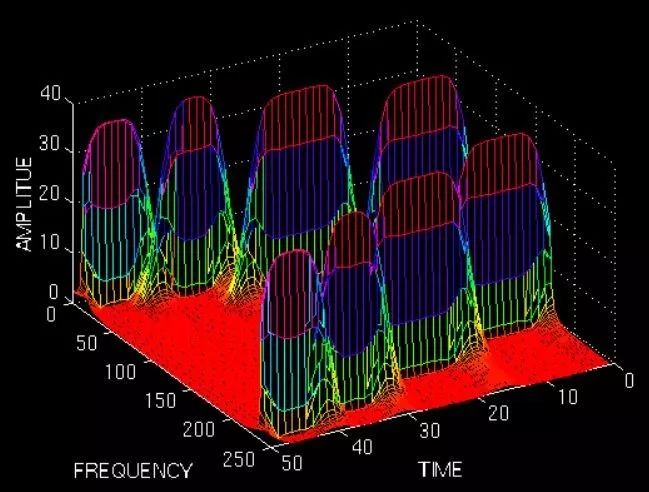
图5. 原始信号的时域和频域分解

四、基于小波分析的堆栈稀疏自编码器网络（Wavelet+SSAE）的总体拓扑结构

考虑到小波分析是时域（空间)和频域内的局部变换，通过伸缩和平移等运算对函数或信号进行多尺度的细化分析，解决了Fourier变换不能解决的许多困难问题，能有效地从输入信号中提取信息，这类变换在金融时间序列数据的处理中能发挥独特优势。对资本市场这类充斥着各种噪音，数据的非平稳、非线性特征十分明显的情形下，我们有必要寻求新的方法、路径来解决这类金融场景的分析、预测问题。为此，我们对自编码器（SSAE）的网络结构进行了改造和重塑，形成了新的深度学习网络结构，改造后的网络结构拓扑图如下：

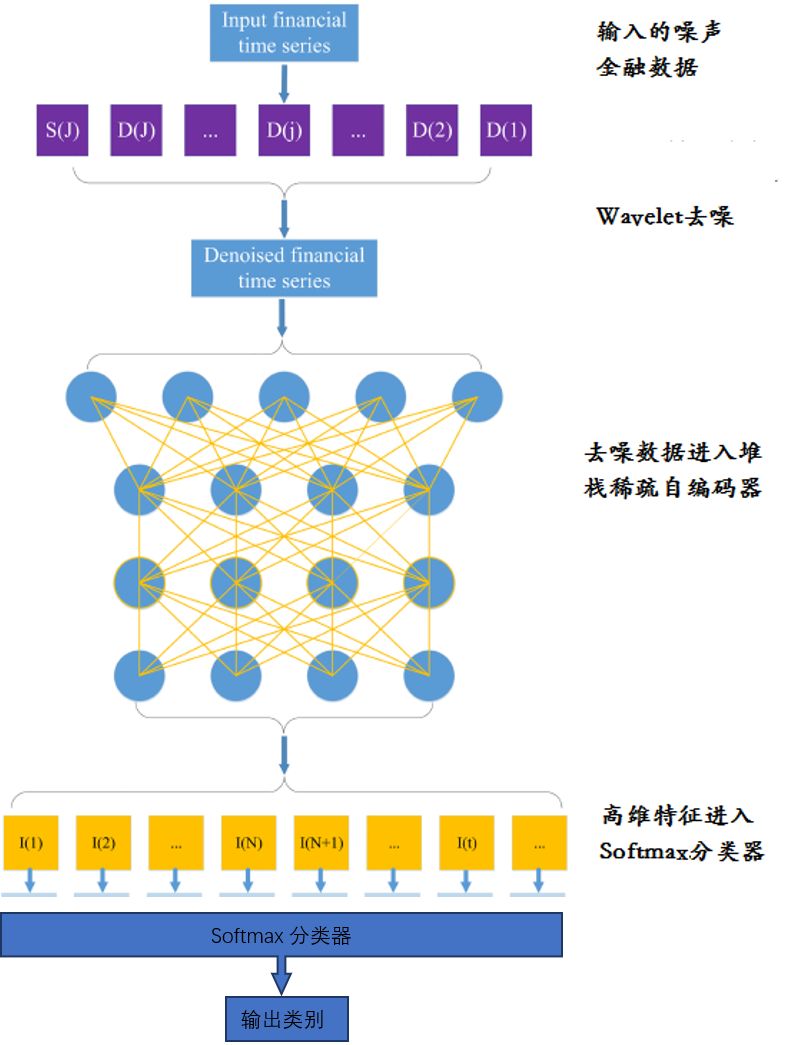
图 6.（Wavelet+SSAE+Softmax）

深度网络拓扑结构

(S(J)为低频信号，D(i)为各尺度的高频信号，

I(i)为编码器提取的高维特征)

具体来说，该新型网络拓扑结构包括输入层，隐含层，输出层，隐含层每层都为稀疏自编码器（SAE），多层稀疏自编码器堆栈（SSAE）组成隐含层。输入层数据首先经过小波去噪，去除数据序列中的高频噪声信号，然后分别经过隐含层的多层自编码器最终提取出稳定，非线性的高维特征，输入Softmax分类器形成最终样本的分类概率。

五、基于Wavelet+SSAE+Softmax应用的场景构建及实验结果

2017年以来市场风格发生了明显变化，沪深300指数涨幅显著高于中证500，大小盘市场走势与以往发生了显著的差异。从2010年开始，中证500累计收益率超过40%，同期沪深300累计收益率则是-6%，而17年收益率发生逆转，中证500下跌了2%，沪深300则涨幅超过20%。对此很多传统市场因子表现失效，这也导致很多量化策略表现不是很理想。据万得统计，2017年量化基金平均收益率1.79%，落后普通股票型基金13倍，特别是近期以来市场波动加剧，诸多策略更是出现了较大回撤。为此，本研究将基于Wavelet+SSAE算法应用于A股全市场的选股，剔除上市不满一年的股票，每周筛选五只股票构建组合并扣除交易手续费，分别以2012年-2017年、以及2017年-2018年7月为不同研究时段，研究不同市场风格下单纯堆栈式自编码器（SSAE）算法及基于小波分析的新型算法对回撤幅度的有效控制程度及相关表现。将以上两种算法在不同市场风格下股票配置组合的回撤进行比较，相关实验结果如下：

（一）2017年市场风格转换前，相关算法配置组合回撤对比

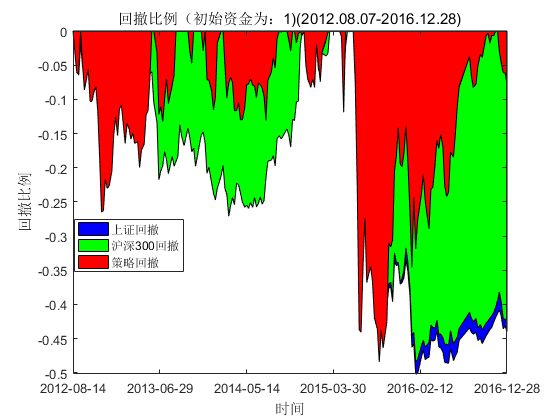
图7.SSAE算法组合持有期内回撤比例

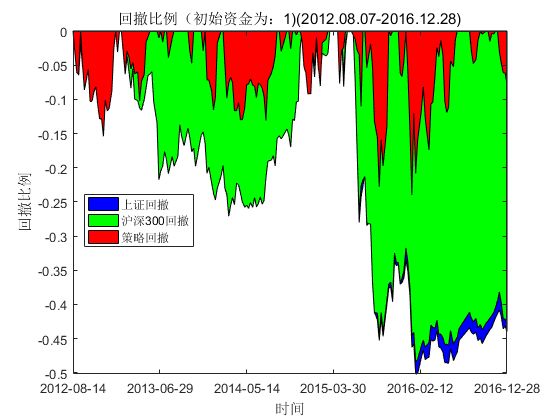
图8. COIF小波+SSAE算法组合持有期内回撤比例

自2015年6月A股从5166高点开始一路下跌到2016年年初2655点，市场的恐慌情绪更是导致2016年年初开盘后2天连续触发4次熔断，上证综指4天跌了将近14%，证监会不得不紧急叫停熔断机制。在此情形下，对比图7、图8进行分析, 实验发现，对比单纯的SSAE的算法与加入Coif小波+SSAE算法两种算法下回撤的变化情况，可以看出通过Coif小波去噪后组合在持有期内（除去2015年6、7月份及2016年初这两段特殊市场情况外）的回撤幅度大都基本控制在10%左右，最大回撤由48%降低为23%，近乎降低了一半（同期上证综指、沪深300的最大回撤为50%），COIF小波+SSAE算法显然比单纯的SSAE算法更具风险控制能力。

（二）2017年市场风格转换后，相关算法配置组合回撤对比

这里的实验研究采用2016.01.01-2017.01.01整年的数据来训练，然后滚动预测2017.01.02-2018.07.03这段时间内的表现，回撤表现如下：

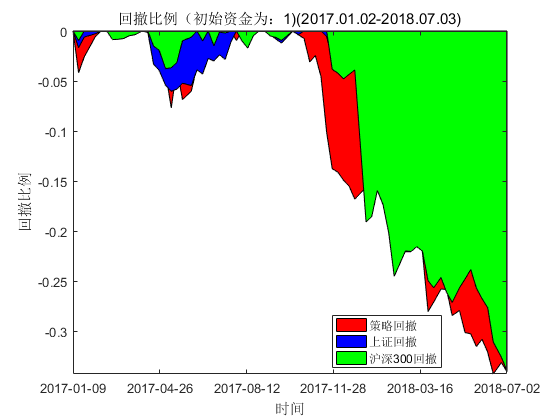
图9.SSAE算法组合持有期内回撤比例

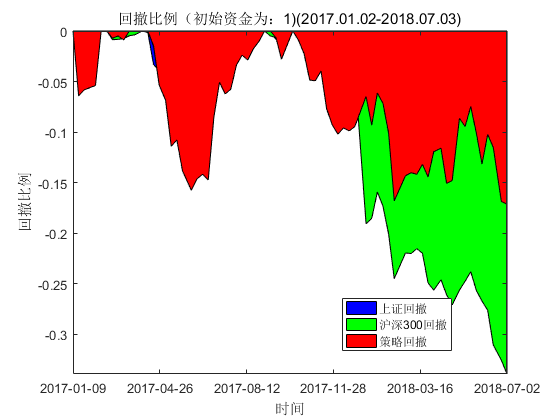
图10. COIF小波+ SSAE算法组合持有期内回撤比例

从图10可知，在风格转换后，COIF小波+SSAE算法推荐组合的最大回撤幅度远小于上证综指和沪深300指数的最大回撤幅度。通过整个持有期内回撤对比发现，通过COIF小波去噪+SSAE算法构造的组合从2017年起截至2018年7月初这段时间内回撤幅度基本控制在15%左右，最大回撤仅17.13%，远低于同期沪深300的33.94%的最大回撤及上证23.62%的最大回撤，COIF小波+SSAE算法呈现出了较强风险控制能力。

应用研究部门：算法金融实验室